Answer:
See Below.
Explanation:
Statements: Reasons:
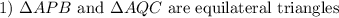 Given
Given
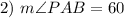 Definition of equilateral.
Definition of equilateral.
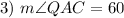 Definition of equilateral.
Definition of equilateral.
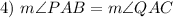 Substitution
Substitution
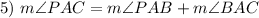 Angle Addition
Angle Addition
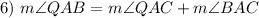 Angle Addition
Angle Addition
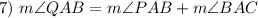 Substitution
Substitution
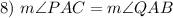 Substitution
Substitution
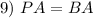 Definition of equilateral
Definition of equilateral
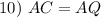 Definition of equilateral
Definition of equilateral
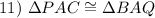 Side-Angle-Side Congruence*
Side-Angle-Side Congruence*
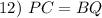 CPCTC
CPCTC
* SAS Congruence:
PA = BA
∠PAC = ∠QAB
AC = AQ