Question

A biologist has been observing a tree's height. This type of tree typically grows by 0.22 feet each month. Fifteen months into the observation, the tree was 20.5 feet tall. Let x be the number of months passed since the observations started, and let y be the tree's height at that time, in feet. Use a linear equation to model the tree's height as the number of months pass. A) This line's slope-intercept equation is: B) 29 months after the observations started, the tree would be [ ] feet in height. С) months after the observation started, the tree would be 29.96 feet tall.

Answer 1

Data:

x: number of months

y: tree's height

Tipical grow: 0.22

Fifteen months into the observation, the tree was 20.5 feet tall: x=15 y=20.5ft (15,20.5)

In this case the slope (m) or rate of change is the tipical grow.

m=0.22

To find the line's slope-intercep equation you use the slope (m) and the given values of x and y (15 , 20.5) in the next formula to find the y-intercept (b):

`\begin{gathered} y=mx+b \\ 20.5=0.22(15)+b \\ 20.5=3.3+b \\ 20.5-3.3=b \\ 17.2=b \end{gathered}`

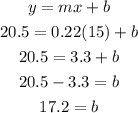
Use the slope(m) and y-intercept (b) to write the equation:

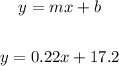
`\begin{gathered} y=mx+b \\ \\ y=0.22x+17.2 \end{gathered}`A) This line's slope-intercept equation is: y=0.22x+17.2

B) To find the height of the tree after 29 months you substitute in the equation the x for 29 and evaluate to find the y:

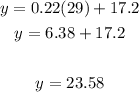
`\begin{gathered} y=0.22(29)+17.2 \\ y=6.38+17.2 \\ \\ y=23.58 \end{gathered}`Then, after 29 months the tree would be 23.58 feet in height

C) In this case as you have the height and need to find the number of moths you substitute the y for 29.96feet and solve the equation for x, as follow:

`\begin{gathered} 29.96=0.22x+17.2 \\ 29.96-17.2=0.22x \\ 12.76=0.22x \\ (12.76)/(0.22)=x \\ \\ 58=x \end{gathered}`Then, after 58 months the tree would be 29.96feet tall