Look yall i got 10 math questions if you get all ten right brainlliest so if yall could help a man out here it would be great
here they are
1.)Which of the following best describes the squaring property of equality?
A.
if a=b,then
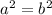
B
if
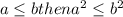
C
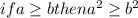
D
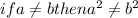
2.)Solve for x.

A.
11
B.
20
C.
83
D
no solution
3.)The length of a side of a square is
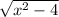
If the area of the square is 12, find x.
A.
16
B.
4
C.
12
D.
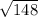
4).Solve for x.
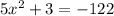
A.
no solution
B.
–5
C.
±5
D.
±25
5.)solve for x

A.
±25
B.
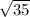
C.
±5
D.
no real solutions
6.)The acceleration of an object can be described by the equation
![image]()
B.

C.
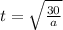
D.

7.)The acceleration of an object can be described by the equation
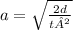
, where a is acceleration, d is the distance, and t is time. Suppose an object accelerates at a rate of 5 meters per second squared. Which of the following equations relates the time of the acceleration to the distance?
A.
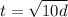
B.
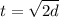
C.
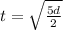
D.
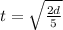
8.)Solve for x
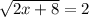
A.
2
B.
–3
C.
–2
D.
no solution
9.)Solve for x:
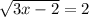
A.
2
B.
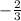
C.
–2
D.
no solution
10.)What is the first step to solve the equation
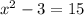
A.
Take the square root of

, 3, and 15.
B.
Square 15.
C.
Add 3 to both sides of the equation.
D.
Add 1 to both sides of the equation.
can yall help a brother out im in deep sh|t if i dont pass so if your gunna do it do it right thank yall for helpen me out oh and i already tried to look em up so that dont work