Question

The graph of g(x) is obtained by reflecting the graph of f(x) = 2x over the x-axis. Which equation describes g(x)?

A. g(x) = -2x + 2
B. g(x) = x + 2
C. g(x) = 22
D. g(x) = -2x

Answer 1

The equation that describes g(x) is g(x) = -2x

Why is this correct?

Upon analyzing the graph of the function
`\( f(x) \)`, the following properties are evident:

`Domain: \( \mathbb{R} \) (All real numbers)`

`Range: \( \{ x \in \mathbb{R} : x \geq 0 \} \)`

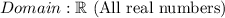
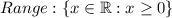
The reflection of
`\( f(x) \)` over the x-axis yields a function that represents the inverse of
`\( f(x) \)`, denoted as
`\( g(x) = -f(x) \)`.

The subsequent transformations are:

`\[ g(x) = -f(x) = [2x] = -2x \]` (utilizing absolute value properties)

Hence, the transformed function
`\( g(x) \)` simplifies to
`\( g(x) = -2x \)` after reflecting
`\( f(x) \)` over the x-axis.

This transformation captures the manipulation applied to the original function
`\( f(x) \)`, resulting in a reflected expression represented by
`\( g(x) \)`.