Question

Kyle paid off his student loan in 3 years by making payments of $750 at the beginning of every month. The interest rate on his loan was 6.70% compounded monthly.

a. Calculate the size of the original loan.
b. Calculate the amount of interest paid on the loan.

Answer 1

The original loan size can be determined by calculating the present value of an annuity with monthly payments of $750 at a 6.70% annual interest compounded monthly over 3 years. To calculate the amount of interest paid, multiply the total number of monthly payments by $750 and subtract the original loan amount.

Step-by-step explanation:

To determine the size of the original loan that Kyle paid off, we can use the present value formula for annuities. Given the monthly payment of $750, an interest rate of 6.70% compounded monthly, and the number of periods (3 years × 12 months per year), we can calculate the present value (PV) of the loan which represents the initial loan amount.

The present value of an ordinary annuity formula is:

`PV = (PMT x (1 - (1 + r)^(^-^n^)))/r`

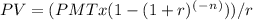
Where PMT is the monthly payment, r is the monthly interest rate (annual rate/12), and n is the total number of payments.

For the second part, calculating the amount of interest paid on the loan, we need to multiply the monthly payment by the number of payments (n) to get the total amount paid and then subtract the original loan amount from this total.