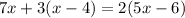Question

)) Which of these equations has infinitely many solutions? 3(2x (2x + 3) = 3x + 1 7x + 3(x - 4) 205x – 6) (x – 8) = x - 5 - 3 -Х 4 Which statement explains a way you can tell the equation has infinitely many solutions? It is equivalent to an equation that has the same variable terms but different constant terms on either side of the equal sign. It is equivalent to an equation that has the same variable terms and the same constant terms on either side of the equal sign. It is equivalent to an equation that has different variable terms on either side of the equation.

Answer 1

An equation has infinitely many solutions when it is equivalent to an equation that has the same variable terms (with the same coefficients on each variable) and the same constant terms on either side of the equal sign.

Simplify the expressions on both sides of each equations to find if they fulfill this criterion.

Equation number 1:

`\begin{gathered} (1)/(2)(2x+3)=3x+1 \\ \Rightarrow x+(3)/(2)=3x+1 \end{gathered}`

This equation does not have the same variable and constant terms on each side.

Equation number 2:

`\begin{gathered} 7x+3(x-4)=2(5x-6) \\ \Rightarrow7x+3x-12=10x-12 \\ \Rightarrow10x-12=10x-12 \end{gathered}`

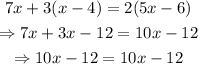
This equation has the same variable and constant terms on each side.

Equation number 3:

`\begin{gathered} (1)/(4)(x-8)=x-5-(3)/(4)x \\ \Rightarrow(1)/(4)x-2=(1)/(4)x-5 \end{gathered}`

This equation does not have the same constant terms on each side.

Therefore, the equation that has infinitely many solutions is the equation number 2:

`7x+3(x-4)=2(5x-6)`