Step-by-step explanation
To find the 1st and 3rd quartile, we must follow the following steps:
1) We order the data from lowest to highest values ✓
2) We look for the median, which gives us the 2nd quartile:
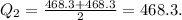
To compute the median, we use the following rule:
• If the size of the data set is ,odd,, do not include the median when finding the first and third quartiles.
,
• If the size of the data set is ,even,, the median is the average of the middle 2 values in the data set. Add those 2 values, and then divide by 2. The median splits the data set into lower and upper halves and is the value of the second quartile Q2.
In this case, the number of elements is n = 54, so it is even.
The median splits the data into two halves.
3) The lower quartile Q1 is the median of the lower half of the data:
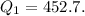
4) The upper quartile Q3 is the median of the upper half of the data.
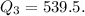
Answer
First quartile: Q_1 = 452.7
Third quartile: Q_3 = 539.5