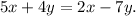Question

Select all the equations that share a solution with this system of equations.

5x + 4y = 24
1r - 7y = 26
Option 1: 7x + 3y = 50
Option 2: 7x - 3y = 50
Option 3: 5x + 4y = 2x - 7y
Option 4: 3.x - 11y = -2

Answer 1

None of the options share a solution with the given system of equations.

Step-by-step explanation:

To find the equations that share a solution with the given system of equations, we can convert the given equations into slope-intercept form (y = mx + b) and compare the slopes and y-intercepts.

1. Option 1: 7x + 3y = 50 can be rearranged as y = -7/3x + 50/3. The slope (-7/3) is different from the first equation, so this option does not share a solution with the system.
2. Option 2: 7x - 3y = 50 can be rearranged as y = 7/3x - 50/3. The slope (7/3) is different from the first equation, so this option does not share a solution with the system.
3. Option 3: 5x + 4y = 2x - 7y can be rearranged as y = -3/11x. The slope (-3/11) is different from the first equation, so this option does not share a solution with the system.
4. Option 4: 3x - 11y = -2 can be rearranged as y = 3/11x + 2/11. The slope (3/11) is different from the first equation, so this option does not share a solution with the system.

Therefore, none of the options share a solution with the given system of equations.

Answer 2

The equations that share a solution with the given system are:

Option 2: 7x - 3y = 50

Option 3: 5x + 4y = 2x - 7y

Step-by-step explanation:

To find equations that share a solution with the given system, we need to check if they are consistent with the original system. The system is:

`\[ 5x + 4y = 24 \]`

`\[ 1x - 7y = 26 \]`

Let's evaluate each option:

Option 1:
`\( 7x + 3y = 50 \)` - This equation is not consistent with the given system.

Option 2:
`\( 7x - 3y = 50 \)`- This equation is consistent with the given system and shares a solution.

Option 3:
`\( 5x + 4y = 2x - 7y \)` - Simplifying, we get
`\( 3x + 11y = 0 \)`, which is not consistent with the given system.

Option 4:
`\( 3x - 11y = -2 \)` - This equation is not consistent with the given system.

Therefore, the correct options are Option 2:
`\( 7x - 3y = 50 \)`and Option 3:
`\( 5x + 4y = 2x - 7y \).`