Question

Passing through (8,-8) and perpendicular to the line whose equation is x-6y-5=0.Write an equation for the line in point slope form and general form.

Answer 1

Given:

The equation of a line is x-6y-5 = 0.

Another line passes perpendicular to the first line through the point (8, -8).

The objective is to find the equation of the second line in point slope form and general form.

Step-by-step explanation:

The general equation of line is,

`y=mx+c\text{ . . . . .(1)}`

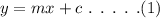
Here, m represents the slope of the line.

To find slope of first line:

The given equation of line 1 can be rewritten as,

`\begin{gathered} x-6y-5=0 \\ -6y=-x+5 \\ y=(-x+5)/(-6) \\ y=(-x)/(-6)+(5)/(-6) \\ y=(x)/(6)-(5)/(6)\text{ . . . . .(2)} \end{gathered}`

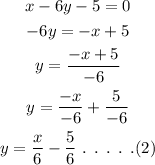
By comparing the equation (2) with the equation (1), the slope of the first line is,

`m_1=(1)/(6)`

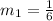
To find slope of line 2:

The slope of line 2 which is perpendicular to line 1 can be calculated as,

`\begin{gathered} m_1* m_2=-1 \\ (1)/(6)* m_2=-1 \\ m_2=-1*6 \\ m_2=-6 \end{gathered}`

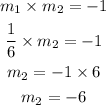
To find equation of line in point slope form:

The general formula of point slope form is,

`y-y_1=m(x-x_1)\text{ . . . . . (3)}`

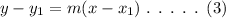
Consider the given coordinate as,

`(x_1,y_1)=(8,-8)`

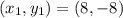
Substitute the value of coordinate and the slope in equation (3),

`\begin{gathered} y-(-8)=-6(x-8) \\ y+8=-6(x-8)\text{ . . . .(4)} \end{gathered}`

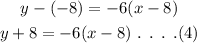
To find equation of line in general form:

The general formula of general form is,

`ax+by+c=0`

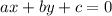
Then, equation (4) can be rewritten as,

`\begin{gathered} y+8=-6x+48 \\ 6x+y+8-48=0 \\ 6x+y-40=0 \end{gathered}`

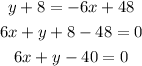
Hence,

The equation of line in point slope form is y +8 = -6(x-8).

The equation of line in general form is 6x + y -40 = 0.