Question

Calculate the mass in grams of V in 4.18 x 10^23 atoms of V.

Answer 1

The mass of vanadium
`(\(V\))` in
`\(4.18 * 10^(23)\)` atoms is approximately
`\(24.38 \, \text{g}\).`

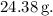
Step-by-step explanation:

To calculate the mass of vanadium
`(\(V\))` in
`\(4.18 * 10^(23)\)` atoms, we use the molar mass of vanadium, which is the mass of one mole of vanadium atoms. The molar mass of vanadium is
`\(50.94 \, \text{g/mol}\).`

First, calculate the number of moles
`(\(n\))` in
`\(4.18 * 10^(23)\)` atoms using Avogadro's number
`(\(6.022 * 10^(23) \, \text{mol}^(-1)\)):`

`\[ n = (4.18 * 10^(23))/(6.022 * 10^(23)) \]`

Next, use the molar mass to find the mass
`(\(m\))` in grams:

`\[ m = n * \text{Molar Mass} \]`

Substitute the values:

`\[ m = (4.18 * 10^(23))/(6.022 * 10^(23)) * 50.94 \]`

Calculating this expression gives the mass of vanadium in grams. Therefore, the mass of
`\(V\)` in
`\(4.18 * 10^(23)\)` atoms is approximately
`\(24.38 \, \text{g}\).`

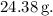
Understanding the concept of molar mass and Avogadro's number is essential in converting between the microscopic scale of atoms or molecules and the macroscopic scale of grams or moles. This calculation is a fundamental step in chemistry for determining the quantity of a substance based on its atomic or molecular composition.