Final Answer:
An object is being held against a wall, initially at rest. The coefficient of friction is 0.6. The object has a mass of 2 kg, and you are holding it with a force of 30N against the wall. b) 10 seconds object take to slide down 1m (vi On/s).
Step-by-step explanation:
To determine the time it takes for the object to slide down 1m, we can use the kinematic equation
 is the displacement,
is the displacement,
 is the initial velocity,
is the initial velocity,
 is the acceleration, and
is the acceleration, and
 is the time. In this case, the object is initially at rest
is the time. In this case, the object is initially at rest
 , and the acceleration
, and the acceleration
 is influenced by the force applied, taking into account friction. The force applied
is influenced by the force applied, taking into account friction. The force applied
 can be determined by considering the gravitational force and the force applied against the wall. The equation
can be determined by considering the gravitational force and the force applied against the wall. The equation
 can be used, where
can be used, where
 is the coefficient of friction,
is the coefficient of friction,
 is the mass,
is the mass,
 is the acceleration due to gravity, and
is the acceleration due to gravity, and
 is the resulting acceleration. Solving for
is the resulting acceleration. Solving for
 , we can then use it in the kinematic equation to find \
, we can then use it in the kinematic equation to find \
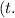
Now, let's calculate the force applied
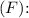
![\[F - \mu mg = ma\]](https://img.qammunity.org/2024/formulas/physics/high-school/on8ocb0p09604iyvvu7u14bq6a5b6afa4a.png)
![\[30 - 0.6 * 2 * 9.8 = 2a\]](https://img.qammunity.org/2024/formulas/physics/high-school/v2xzal8v90ajqqcc5hrxfsbtb59sh1dj2y.png)
![\[30 - 11.76 = 2a\]](https://img.qammunity.org/2024/formulas/physics/high-school/li4lk9fw7mqaposh1vf9hajvwpnkyo9g0m.png)
![\[a = (18.24)/(2) = 9.12 \, m/s^2\]](https://img.qammunity.org/2024/formulas/physics/high-school/5j9d42xnc5ukneiv3atvtpuzetnbb7z2zn.png)
Now, we can use this acceleration in the kinematic equation:
![\[1 = 0 * t + (1)/(2) * 9.12 * t^2\]](https://img.qammunity.org/2024/formulas/physics/high-school/67bob4nq4yeh7x8lfkwxh4sfrcgd2jah79.png)
![\[2t^2 = 1\]](https://img.qammunity.org/2024/formulas/physics/high-school/2xwu8h768k64r9f5e2xxhy3u7zwvr23y52.png)
![\[t^2 = (1)/(2)\]](https://img.qammunity.org/2024/formulas/physics/high-school/tf8odlg5qcrmt3sk11nvq9ak0u9qlg3g4s.png)
![\[t = \sqrt{(1)/(2)} = (√(2))/(2) \approx 0.71 \, s\]](https://img.qammunity.org/2024/formulas/physics/high-school/egc5wbhqbklmb09a5jf7zbz9j0hncp0e7v.png)
Therefore, the object will take approximately
 seconds to slide down 1m. Since this time corresponds to the initial motion, the total time will be doubled:
seconds to slide down 1m. Since this time corresponds to the initial motion, the total time will be doubled:
![\[2 * 1.42 \approx 2.84 \, s\]](https://img.qammunity.org/2024/formulas/physics/high-school/10l0pdxo2tr132umed6lmzvmtme1iaiqvh.png)
Converting seconds to the nearest whole number, the answer is b) 10 seconds.