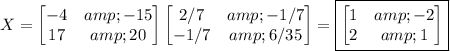Question

Solve the matrix equation for X:

Answer 1

Multiply on the right by the transpose of the matrix on the left side:

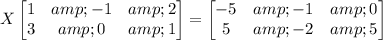
`X\begin{bmatrix}1&-1&2\\3&0&1\end{bmatrix}=\begin{bmatrix}-5&-1&0\\5&-2&5\end{bmatrix}`

The transpose is just the same matrix with the entries reflected along the main diagonal:

`\begin{bmatrix}1&-1&2\\3&0&1\end{bmatrix}^\top=\begin{bmatrix}1&3\\-1&0\\2&1\end{bmatrix}`

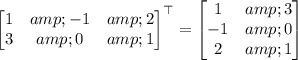
So

`X\begin{bmatrix}1&-1&2\\3&0&1\end{bmatrix}\begin{bmatrix}1&3\\-1&0\\2&1\end{bmatrix}=\begin{bmatrix}-5&-1&0\\5&-2&5\end{bmatrix}\begin{bmatrix}1&3\\-1&0\\2&1\end{bmatrix}`

`X\begin{bmatrix}6&5\\5&10\end{bmatrix}=\begin{bmatrix}-4&-15\\17&20\end{bmatrix}`

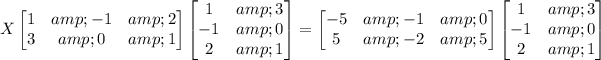
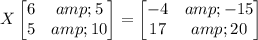
Now multiply on the right by the inverse of the matrix on the left side:

`X\begin{bmatrix}6&5\\5&10\end{bmatrix}\begin{bmatrix}6&5\\5&10\end{bmatrix}^(-1)=\begin{bmatrix}-4&-15\\17&20\end{bmatrix}\begin{bmatrix}6&5\\5&10\end{bmatrix}^(-1)`

`X=\begin{bmatrix}-4&-15\\17&20\end{bmatrix}\begin{bmatrix}6&5\\5&10\end{bmatrix}^(-1)`

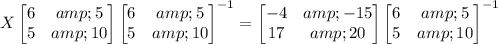
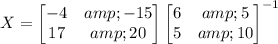
The inverse is

`\begin{bmatrix}6&5\\5&10\end{bmatrix}^(-1)=\frac1{60-25}\begin{bmatrix}10&-5\\-5&6\end{bmatrix}=\begin{bmatrix}2/7&-1/7\\-1/7&6/35\end{bmatrix}`

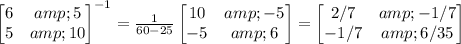
So

`X=\begin{bmatrix}-4&-15\\17&20\end{bmatrix}\begin{bmatrix}2/7&-1/7\\-1/7&6/35\end{bmatrix}=\boxed{\begin{bmatrix}1&-2\\2&1\end{bmatrix}}`