Question

In 2026, Darius invested $7,000 into an account paying 2% interest compounded annually. What will be his balance in the year 2029?

Answer 1

Darius' balance in 2029 after investing $7,000 at 2% interest compounded annually for 3 years will be approximately $7,428.46.

Step-by-step explanation:

Calculating Compound Interest

Darius invested $7,000 in an account paying 2% interest compounded annually. The balance in the year 2029 can be calculated using the compound interest formula, which is
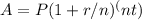`A = P(1 + r/n)^(nt)`. In this case, 'A' is the amount of money accumulated after n years, including interest. 'P' is the principal amount (the initial amount of money), 'r' is the annual interest rate (decimal), 'n' is the number of times that interest is compounded per year, and 't' is the time the money is invested for in years.

For Darius' investment:

P = $7,000 (the initial amount invested)

r = 2% or 0.02 (annual interest rate)

n = 1 (since the interest is compounded annually)

t = 2029 - 2026 = 3 years

Plugging the values into the formula, we get:

`A = $7,000(1 + 0.02/1)^(1*3)`

`A = $7,000(1 + 0.02)^3`

`A = $7,000(1.02)^3`

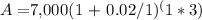
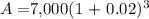
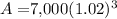
A = $7,000(1.061208)

A ≈ $7,428.46

Therefore, the balance in Darius' account in the year 2029 will be approximately $7,428.46.