The perimeter will increase proportional to the value of x. We can write the perimeter in function of x as:
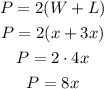
Then, if x=8, the perimeter is:
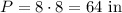
If we increase x by 2, we will have x=8+2=10, and the perimeter will be:
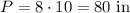
Answer:
For x=8, the perimeter is P=64.
For x=10, the perimeter is P=80 (it is increased by 8*2=16 units)