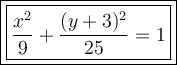Question

Find an equation of the ellipse that has center (0, -3), a major axis of length 10, and endpoint of minor axis (-3, -3).

Answer 1

The equation of an ellipse with center (h, k), semi-major axis a, and semi-minor axis b is ((x-h)^2)/(a^2) + ((y-k)^2)/(b^2) = 1.

Step-by-step explanation:

To find the equation of the ellipse, we need to determine the values of a and b.

Since the major axis has a length of 10, we can determine the value of a by dividing the length by 2, giving us a = 10/2 = 5.

The endpoint of the minor axis is (-3,-3), which means that the length of the minor axis is 6.

Therefore, b = 6/2 = 3.

The equation of an ellipse with center (h, k), semi-major axis a, and semi-minor axis b is given by:

=> ((x-h)^2)/(a^2) + ((y-k)^2)/(b^2) = 1

Plugging in the values, we have ((x-0)^2)/(5^2) + ((y+3)^2)/(3^2) = 1. This is the equation of the ellipse.

Answer 2

`(x^2)/(9)+((y+3)^2)/(25)=1`

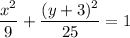
Step-by-step explanation:

We are told that the center of the ellipse is (0, -3) and the endpoint of the minor axis is (-3, -3). Since the y-coordinates of the center and the minor axis are the same, the ellipse is vertical.

The general equation of a vertical ellipse is:

`\boxed{\begin{array}{l}\underline{\textsf{General equation of a vertical ellipse}}\\\\((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1\\\\\textsf{where:}\\\phantom{ww}\bullet\textsf{$2b=$ major axis}\\\phantom{ww}\bullet\textsf{$2a=$ minor axis}\\\phantom{ww}\bullet \textsf{$(h,k)=$ center}\\\phantom{ww}\bullet\textsf{$(h,k\pm b)=$ major vertices}\\\phantom{ww}\bullet\textsf{$(h\pm a,k)=$ minor vertices}\\\phantom{ww}\bullet\textsf{$(h,k\pm c)=$ foci where $c^2=b^2-a^2$}\end{array}}`

Given that the center is (0, -3):

• h = 0
• k = -3

Given that the major axis (2b) is 10 units in length:

• b = 5

The minor axis (2a) of a vertical ellipse is the horizontal distance between the two points on the ellipse that are farthest apart along the shorter axis. The center of the ellipse is the midpoint of the minor axis. Therefore, the value of a can be found by taking the positive difference of the x-coordinates of the center and the minor axis endpoint:

`a=|0-(-3)|=3`

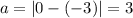
Therefore, a = 3.

Substitute the values of h, k, a and b into the equation of the ellipse:

`((x-0)^2)/(3^2)+((y-(-3))^2)/(5^2)=1`

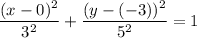
Simplify:

`(x^2)/(9)+((y+3)^2)/(25)=1`

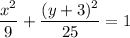
Therefore, the equation of the ellipse that has center (0, -3), a major axis of length 10, and endpoint of minor axis (-3, -3) is:

`\large\boxed{\boxed{(x^2)/(9)+((y+3)^2)/(25)=1}}`