Question

Given: cosA = -24/25, sinB = 3/5, and are second-quadrant angles; find cos(A - B)

A: 117/125.
B: 3/5.
C: 4/5.

Answer 1

A

Step-by-step explanation:

note : in the second quadrant

• cosA and cosB < 0

• sinA and sinB > 0

---------------------------------

given

cosA = -
`(24)/(25)` = -
`(adjacent)/(hypotenuse)`

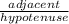
This is a 7 - 24 - 25 right triangle

with opposite side 7 , adjacent side 24 and hypotenuse 25

then

sinA =
`(opposite)/(hypotenuse)` =
`(7)/(25)`

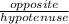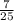
given

sinB =
`(3)/(5)` =
`(opposite)/(hypotenuse)`

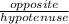
This is a 3 - 4 - 5 right triangle

with opposite side 3, adjacent side 4 and hypotenuse 5

then

cosB = -
`(adjacent)/(hypotenuse)` = -
`(4)/(5)`

---------------------------------------------------------

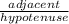using the addition formula for cosine

• cos(A ± B ) = cosAcosB ∓ sinAsinB

Then

cos(A - B)

= cosAcosB + sinAsinB

= -
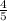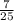`(24)/(25)` × -
`(4)/(5)` +
`(7)/(25)` ×
`(3)/(5)`

=
`(96)/(125)` +
`(21)/(125)`

=
`(117)/(125)`

Answer 2

The value of cos(A - B) is -12/125.

Step-by-step explanation:

We can use the trigonometric identity for cosine of the difference of two angles to find cos(A - B). The identity is given by:

cos(A - B) = cosA * cosB + sinA * sinB

Now, we substitute the given values into the formula:

cos(A - B) = (-24/25) * cosB + (3/5) * sinB

We can simplify this:

cos(A - B) = (-24/25) * (3/5) + (3/5) * (4/5)

cos(A - B) = -72/125 + 12/25

cos(A - B) = -72/125 + 60/125

cos(A - B) = -12/125

Therefore, the answer is -12/125.