Question

Explain how to find the 16th term of the sequence defined by the explicit rule n^2+ 6. Assume that the domain of the function is the set of whole numbers greater than 0.​

Answer 1

To find the 16th term of the sequence, substitute the value of n into the formula n² + 6.

Step-by-step explanation:

To find the 16th term of the sequence defined by the explicit rule n² + 6, we need to plug in the value of n as 16 into the formula n² + 6.

So, the 16th term is 16² + 6 = 256 + 6 = 262.

Answer 2

The 16th term of the sequence defined by the explicit rule
`n^2` + 6 where the domain is the set of whole numbers greater than 0 is 262.

Step-by-step explanation:

To find the 16th term of the sequence defined by the explicit rule
`n^2` + 6 for whole numbers greater than 0, substitute n = 16 into the formula
`n^2`+ 6 to calculate the value.

Upon substituting n = 16 into the formula
`n^2` + 6, we get 1
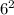`6^2` + 6 = 262, which represents the 16th term of the sequence.

The explicit rule
`n^2` + 6 denotes a sequence where each term is obtained by substituting consecutive whole numbers greater than 0 into the formula. In this case, finding the 16th term necessitates substituting n = 16 into the formula to evaluate the value.

The term-by-term application of the formula
`n^2` + 6 for n = 1, 2, 3, ...) results in a sequence of numbers, with each term being the square of its respective n value increased by 6.

Substituting n = 16 into the formula
`n^2` + 6 to compute the 16th term follows the same pattern established by the rule, generating the value 262 as the 16th term in the sequence.

Therefore, by substituting n = 16 into the explicit rule
`n^2` + 6, we ascertain that the 16th term in the sequence is 262.