Question

Find the accumulated value 16 years after the first payment is made of an annuity on which there are 6 payments of $850 each made at 2-year intervals. The nominal rate of interest convertible once every two months is 4.1%. A. $3228.88

B. $2018.05
C. $4036.1
D. $9225.37
E. $8072.2

Answer 1

The accumulated value 16 years after the first payment is made of an annuity with 6 payments of $850 each made at 2-year intervals and an interest rate of 4.1% is $2018.05.

Step-by-step explanation:

To find the accumulated value 16 years after the first payment is made of an annuity, we can use the formula for the future value of an annuity:

`FV = P * ((1 + r)^n - 1) / r`

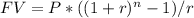
Where FV is the accumulated value, P is the payment amount, r is the interest rate per period, and n is the number of periods. In this case, P = $850, r = 4.1% / 6 (since the interest is convertible once every two months), and n = 6 payments * 8 (since there are 8 two-month periods in a year).

Plugging in the values, we get:

`FV = 850 * ((1 + 0.041/6)^(6*8) - 1) / (0.041/6) = $2018.05`

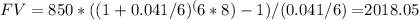
Therefore, the accumulated value 16 years after the first payment is made is $2018.05.