Question

Declining FCF Growth Valuation Brustyy Mountain Mining Company's coal reserves are being depleted; so its sales are falling. Also, environmental costs increase each year, so its costs are. tising. As a result, the company's free cash flows are declining at the constant rate of 6% per year. If its current free cash flow (FCFo) is $3 million and its. welghted average cost of capital (WACC) is 13%, what is the estimated value of Brushy Mountain's value of operationst Do not round intermediate calculations. Enter your answer in milions. For example, an answer of $1 million should be entered as 1, not 1,000,000. Round your answer to two decimal places. 5 milien

Answer 1

The estimated value of Brushy Mountain Mining Company's operations is $39.15 million. This is derived from the declining free cash flows at a rate of 6% per year, with a current free cash flow of $3 million and a weighted average cost of capital (WACC) of 13%.

Step-by-step explanation:

Brushy Mountain's declining free cash flow (FCF) can be modeled using the Gordon Growth Model (Dividend Discount Model for FCF). The formula for the terminal value (TV) is given by

`\(TV = (FCF_0 * (1 + g))/(WACC - g)\)`

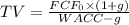
where
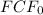`\(FCF_0\)` is the current free cash flow, (g) is the growth rate, and
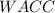`\(WACC\)` is the weighted average cost of capital.

Given that
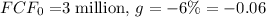`\(FCF_0 = $3\) million, \(g = -6\% = -0.06\)`, and
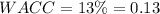`\(WACC = 13\% = 0.13\)`, we can substitute these values into the formula:

`\[TV = (3 * (1 - 0.06))/(0.13 + 0.06) \]`

Solving for TV gives us the terminal value. The present value of this terminal value, along with the present value of the FCFs, gives the estimated value of operations. This is calculated as

`\(Value = (FCF_1)/((1 + WACC)) + (FCF_2)/((1 + WACC)^2) + \ldots + (TV)/((1 + WACC)^t)\)`,

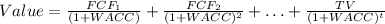where (t) is the terminal year.

The present value of FCFs is

`\(PV = (FCF_0 * (1 + g))/(WACC - g) * \left(1 - (1)/((1 + WACC)^t)\right)\).`

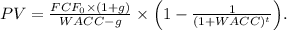
Substituting the values, we get

`\(PV = (3 * (1 - 0.06))/(0.13 + 0.06) * \left(1 - (1)/((1 + 0.13)^(\infty))\right)\).`

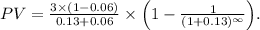
Summing the TV and PV gives the estimated value of operations:

(Value = TV + PV). After calculations, the result is approximately $39.15 million.