Question

3. At Carl's Cambie Diner, there are three sizes of coffee drinks: regular (300 mL), large (500 mL) and extra large (800 mL), and they cost $2.25, $3.25 and $5.75, respectively. On a particular afternoon, the diner sold a total of 37 coffees. The total volume of coffee sold was 19,100 mL and the amount of money made in coffee sales was $133.25. How many of each size of drink did customers buy that afternoon? Variables: Equations: Solve:

Answer 1

12 regular

15 large

10 extra large

Step-by-step explanation:

Variables:

s = number of coffees with regular size

l = number of coffees with large size

e = number of coffees with extra large size

Equations.

Equation for the quantity of coffees sold:

we add all of the quantities s, l and e:

`s+l+e=37`

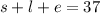
this is because the diner sold a total of 37 coffees. This will be equation 1.

Equation for the volume of coffee:

We need to multiply the volume that each side has with the number of coffees with that size:

`300s+500l+800e=19100`

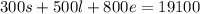
This is because the total volume of coffee sold was 19100mL. This will be equation 2.

Equation for the coffee sales:

We multiply the price of each coffee by the amount of coffes with that price:

`2.25s+3.25l+5.75e=133.25`

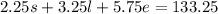
This is because the small cost $2.25, the large $3.25 and the extra large $5.75, and the total of coffee sales was $133.25. This will be equation 3.

Solve.

There are many ways to solve a 3 variable system of equations. I will multiply the first equation by -300 to add it to the second equation and eliminate s.

Multiply 1 by -300:

`\begin{gathered} -300(s+l+e=37) \\ -300s-300l-300e=-11,100 \end{gathered}`

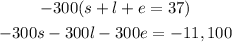
Now we add this to equation 2

`\begin{gathered} -300s-300l-300e=-11,100 \\ 300s+500l+800e=19,100 \\ ---------------- \\ 200l+500e=8,000 \end{gathered}`

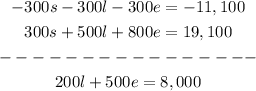
I will call this equation 4.

Next, we will use equation 2 and equation 3 to eliminate the same variable s, for this we multiply equation 2 by -2.25

`\begin{gathered} -2.25(300s+500l+800e=19,100) \\ -675s-1,125l-1,800=-42,975 \end{gathered}`

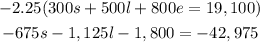
and equation 3 by 300:

`\begin{gathered} 300(2.25s+3.25l+5.75e=133.25) \\ 675s+975l+1,725e=39,975 \end{gathered}`

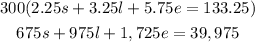
And we add this two equations to elimate s:

`\begin{gathered} -675s-1,125l-1,800=-42,975 \\ 675s+975l+1,725e=39,975 \\ ----------------- \\ -150l-75e=-3,000 \end{gathered}`

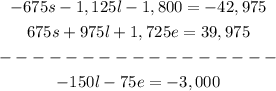
This will be equation 5.

Now we use equations 4 and 5 to find l and e. For that, we multiply equation 5 by 4/3:

`\begin{gathered} (4)/(3)(-150l-75e=-3,000) \\ -200l-100e=-4,000 \end{gathered}`

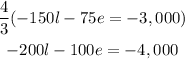
And add this to equation 4:

`\begin{gathered} 200l+500e=8,000 \\ -200l-100e=-4,000 \\ ----------- \\ 400e=4,000 \\ e=4,000/400 \\ e=10 \end{gathered}`

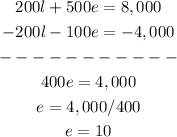
We have the value of e. Now we substitute this into equation 5, to solve for l:

`\begin{gathered} -150l-75e=-3,000 \\ -150l-75(10)=-3,000 \\ -150l-750=-3,000 \\ -150l=-3,000+750 \\ -150l=-2,250 \\ l=-2,250/(-150) \\ l=15 \end{gathered}`

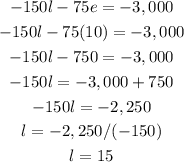
We have tha value of l, now we need to substitute e and l into equation 1 to find s:

`\begin{gathered} s+l+e=37 \\ s+15+10=37 \\ s+25=37 \\ s=37-25 \\ s=12 \end{gathered}`

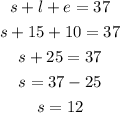
Answer:

12 regular

15 large

10 extra large