Question

A $150,000 mortgage is amortized over 25 years. If interest on the mortgage is 3.5 percent compounded semi-annually, calculate the size of monthly payments made at the end of each month.

A. $784.91
B. $748.91
C. $734.91
D. $743.91

Answer 1

The correct monthly payment for a $150,000 mortgage amortized over 25 years with a 3.5 percent interest rate compounded semi-annually is approximately $734.91 (Option C).

Step-by-step explanation:

To calculate the monthly payment, we can use the formula for the monthly payment on an amortizing loan, which is given by:

`\[M = P * (r(1 + r)^n)/((1 + r)^n - 1)\]`

Where:

- M is the monthly payment,

- P is the principal amount (loan amount),

- r is the monthly interest rate (annual rate divided by 12),

- n is the total number of payments (loan term in years multiplied by 12).

For this mortgage:

- P = $150,000,

-
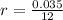`\(r = (0.035)/(12)\)`(monthly interest rate),

-
`\(n = 25 * 12\)`(25 years amortized monthly).

Now, substituting these values into the formula:

`\[M = 150000 * ((0.035)/(12) * \left(1 + (0.035)/(12)\right)^(25 * 12))/(\left(1 + (0.035)/(12)\right)^(25 * 12) - 1)\]`

After solving this expression, the monthly payment comes out to be approximately $734.91. Therefore, the correct answer is $734.91 (Option C). This represents the amount the borrower needs to pay at the end of each month to fully amortize the loan over 25 years with a 3.5 percent interest rate compounded semi-annually.