Question

a store selling two mixtures of nuts in 20 oz bags. the first mixture has 15 oz of peanuts combined with 5 oz of cashews, and cost $6. the second mixture has 5 oz of peanuts and 15 oz of cashews, and cost $8. how much does 1 oz of peanuts and 1 oz of cashews cost.

Answer 1

We can solve this using a system of equations.

Let p be the price of 1 ounce of peanuts and c be the price of 1 ounce of cashews.

"...the first mixture has 15 oz of peanuts combined with 5 oz of cashews, and cost $6." gives us our first equation, that is:

`15p+5c=6`

"...the second mixture has 5 oz of peanuts and 15 oz of cashews, and cost $8." gives us our second equation, that is:

`5p+15c=8`

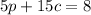
Thereby, the system would be:

`\begin{cases}15p+5c=6 \\ 5p+15c=8\end{cases}`

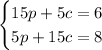
Let's mulitply the first equation by -3 and add both of them up:

`\begin{cases}15p+5c=6 \\ 5p+15c=8\end{cases}\rightarrow\begin{cases}-45p-15c=-18 \\ 5p+15c=8\end{cases}\rightarrow-40p=-10`

Solving for p,

`\begin{gathered} -40p=-10\rightarrow p=(-10)/(-40)^{} \\ \Rightarrow p=0.25 \end{gathered}`

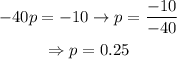
Let's plug in this value in equation 2 and solve for c, as following:

`\begin{gathered} 5p+15c=8 \\ \rightarrow5(0.25)+15c=8\rightarrow1.25+15c=8\rightarrow15c=6.75\rightarrow c=(6.75)/(15) \\ \\ \Rightarrow c=0.45 \end{gathered}`

This way, we would have that

`\begin{gathered} p=0.25 \\ c=0.45 \end{gathered}`

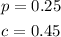
Meaning that an ounce of peanuts costs $0.25, and an ounce of cashews costs $0.45