Question

A flashlight contains two batteries connected in series with a small bulb. When the switch is closed, the current in the circuit is I. If the circuit is changed so that two identical bulbs are connected in series to the same two batteries, what is the current?

Answer 1

Given:

The initial value of the current through the circuit is I.

To find:

The current through the circuit after the circuit is changed.

Step-by-step explanation:

Let us assume that the total voltage supplied by the two batteries to the circuit is V.

And let us assume that the resistance of the bulb is R.

From Ohm's law, the voltage across the circuit is given by,

`V=IR`

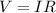
Thus the current will be,

`I=(V)/(R)\text{ }\rightarrow\text{ \lparen i\rparen}`

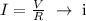
When the two identical bulbs are connected, the total resistance of the circuit will be R+R=2R.

Thus from Ohm's law, the current through the resistance is given by,

`I_0=(V)/(2R)`

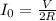
On substituting the equation (i) in the above equation,

`\begin{gathered} I_0=(I)/(2) \\ I_0=(1)/(2)I \end{gathered}`

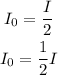
Final answer:

The current in the circuit after the circuit is changed is (1/2) I.