Final answer:
The value of each bond can be calculated using the present value formula. At different interest rates, the values of the bonds will vary. Bond L will have a higher value with lower interest rates and a lower value with higher interest rates. Bond S, with a shorter maturity period, will have a lower value compared to Bond L at the same interest rates.
Step-by-step explanation:
To calculate the value of each bond at different interest rates, we can use the present value formula. The formula for the present value of a bond is:
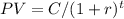
Where PV is the present value, C is the annual coupon payment, r is the interest rate, and t is the number of years until maturity. Let's calculate the value of each bond at an interest rate of 6%, 8%, and 12%:
- Bond L (12-year maturity) at 6% interest rate:
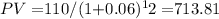
- Bond L (12-year maturity) at 8% interest rate:
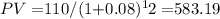
- Bond L (12-year maturity) at 12% interest rate:
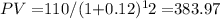
- Bond S (1-year maturity) at 6% interest rate:
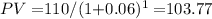
- Bond S (1-year maturity) at 8% interest rate:
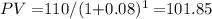
- Bond S (1-year maturity) at 12% interest rate:
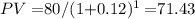
Therefore, the value of each bond for different interest rates is as follows:
- Bond L: $713.81 (6%), $583.19 (8%), $383.97 (12%)
- Bond S: $103.77 (6%), $101.85 (8%), $71.43 (12%)