Question

Write a system of equations to describe the situation below, solve using elimination, and fill in the blanks.Kenneth is thinking of two numbers. Adding 4 times the first number and 7 times the second number gives a total of -9. Also, adding 3 times the first number and 9 times the second number gives -3. What are the two numbers?

Answer 1

Let x and y be the first and second number, respectively. Then, the statement "adding 4 times the first number and 7 times the second number gives a total of -9" can be written as

`4x+7y=-9`

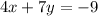
and the statement "adding 3 times the first number and 9 times the second number gives -3" can be written as

`3x+9y=-3`

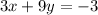
Therefore, the system of equations is:

`\begin{gathered} 4x+7y=-9 \\ 3x+9y=-3 \end{gathered}`

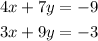
Solving by elimination method.

By multiplying by -3 the first equation and by 4 the second one, we obtain an equivalent system of equations:

`\begin{gathered} -12x-21y=27 \\ 12x+36y=-12 \end{gathered}`

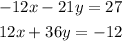
Then, by adding both equations, we get

`\begin{gathered} 36y-21y=27-12 \\ \text{which gives} \\ 15y=15 \end{gathered}`

So, y is given by

`\begin{gathered} y=(15)/(15) \\ y=1 \end{gathered}`

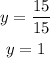
Finally, we can find x by substituting this value into the second equation of our system. It yields,

`3x+9(1)=-3`

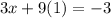
which gives

`\begin{gathered} 3x+9=-3 \\ 3x=-12 \\ \text{then} \\ x=(-12)/(3) \\ x=-4 \end{gathered}`

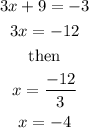
Therefore, the two numbers are: 1 and -4.