Question

Maria, who is now 52 years old, is employed by a firm that guarantees her a pension of $45,000/year at age 65. What is the present value of her first year's pension if the inflation over the next 13 years is 3%/year compounded continuously? 4%/year compounded continuously? 6%/year compounded continuously?

Answer 1

• a) The present value of Maria's first year's pension is approximately $30,459.58 with a 3% inflation rate compounded continuously,
• b) The present value of Maria's first year's pension is approximately $26,829.83 with a 4% inflation rate compounded continuously, and
• c) The present value of Maria's first year's pension is approximately $20,626.99 with a 6% inflation rate compounded continuously.

Step-by-step explanation:

To find the present value of Maria's first year's pension, we need to discount the future value (pension amount at age 65) back to the present using the given inflation rates and continuous compounding.

First, let's calculate the number of years from the present (52 years old) to when Maria turns 65. This is 65 - 52 = 13 years.

Next, we'll use the continuous compounding formula:

PV = FV / e⁽ʳ*ᵗ⁾

where PV is the present value, FV is the future value, r is the interest rate, and t is the time in years.

a) For an inflation rate of 3% year compounded continuously:

`PV = $45,000 / e^((0.03*13)) = $45,000 / e^((0.39)) =$45,000 / 1.477 =$30,459.58`

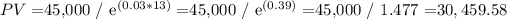
b) For an inflation rate of 4% year compounded continuously:

`PV = $45,000 / e^((0.04*13)) = $45,000 / e^((0.52)) = $45,000 / 1.678= $26,829.83`

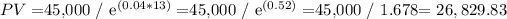
c) For an inflation rate of 6% year compounded continuously:

`PV = $45,000 / e^((0.06*13)) = $45,000 / e^((0.78)) = $45,000 / 2.181 =$20,626.99`

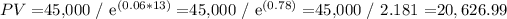
Therefore, the present value of Maria's first year's pension is approximately:

• - $30,459.58 with a 3% inflation rate compounded continuously,
• - $26,829.83 with a 4% inflation rate compounded continuously, and
• - $20,626.99 with a 6% inflation rate compounded continuously.