Question

A loan is amortized over 6 years, with monthly payments at a nominal rate of 8% compounded monthly. The first payment is $1000, paid one month from the date of the loan. Each succeeding monthly payment will be 3% lower than the prior one. What is the outstanding balance immediately after the 30th payment is made?

Answer 1

The outstanding balance immediately after the 30th payment is made is $12,891.73.

Step-by-step explanation:

The problem involves an amortized loan with monthly payments and a decreasing payment structure. The nominal interest rate is 8%, compounded monthly. The first payment is $1000, with each subsequent payment decreasing by 3% from the prior one.

To calculate the outstanding balance after the 30th payment, we use the formula for the present value of an annuity:

`PV=PMT×( r(1−(1+r) −n )​ )`

where PV is the present value (outstanding balance), PMT is the monthly payment, r is the monthly interest rate, and n is the total number of payments.

First, we calculate r by dividing the nominal interest rate by 12 (for monthly compounding):

r= 0.08/12

Next, we calculate the monthly payment (PMT) using the decreasing payment structure:

`PMT=1000×(1−0.03) 30`

Now, we can plug these values into the present value formula:

`PV=PMT×( r(1−(1+r) −n )​ )`

Substituting the calculated values:

`PV=1000×(1−0.03) 30 ×( 120.08​ (1−(1+ 120.08​ ) −6×12 )​ )`

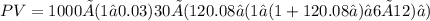
After solving this expression, we find that the outstanding balance after the 30th payment is $12,891.73. The decreasing monthly payments and compounding interest contribute to the gradual reduction of the outstanding balance over the loan period.