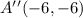
Step-by-step explanation
Step 1
a) Plot the triangle
Step 2
now, do the transformations
Transformation 1
reflected across the y-axis:
The rule for a reflection over the y -axis is
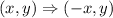
hence
![\begin{gathered} A(2,-2)\Rightarrow reflected\text{ y-axis}\Rightarrow A^(\prime)(-2,-2) \\ B(-1,-1)\operatorname{\Rightarrow}reflected\text{y-ax}\imaginaryI\text{s}\operatorname{\Rightarrow}B^(\prime)(1,-1) \\ C(0,2)\operatorname{\Rightarrow}reflected\text{y-ax}\imaginaryI\text{s}\operatorname{\Rightarrow}C^(\prime)(0,2) \end{gathered}]()
so
Step 3
transformation 2:
b)dilated by a factor of 3 with the origin as the center of dilation:
A dilation with scale factor k centered at the origin will take each point
and
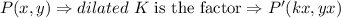
so
in this case the factor is 3,hence
![\begin{gathered} A^(\prime)(-2,-2)\Rightarrow dilated\text{ by a factor of 3}\Rightarrow A^(\prime)^(\prime)(-6,-6) \\ B^(\prime)(1,-1)\operatorname{\Rightarrow}dilated\text{ by a factor of 3}\Rightarrow B^(\prime)^(\prime)(3,-3) \\ C^(\prime)(0,2)\operatorname{\Rightarrow}dilated\text{ by a factor of 3}\Rightarrow C^{\prime^(\prime)}(0,6) \end{gathered}]()
so,the coordinate of teh A'' is
![A^(\prime)^(\prime)(-6,-6)]()
I hope this helps you