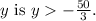Final Answer:
The type of compound inequality represented by
 is a "greater than" compound inequality.
is a "greater than" compound inequality.
Step-by-step explanation:
Certainly! Let's go through the detailed calculations and explanation for the given compound inequality:
The original inequality is
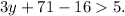
Step 1: Combine like terms on the left side of the inequality:
![\[3y + 71 - 16 > 5\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6igdnr0z5rzx8hqbrh1wi6sfd5a50gv4fb.png)
Combine the constants (71 and -16):
![\[3y + 55 > 5\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/li39cm1idnbjts54tik1hg7mjokqp5mjtj.png)
Step 2: Subtract 55 from both sides to isolate the
 term:
term:
![\[3y > -50\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/crzm6qaz6uk5i3so99ve4x7ne7kk7kpbdo.png)
Step 3: Divide both sides by 3 to solve for
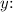
![\[y > -(50)/(3)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ivydb8oh7g1lwkrzks2wnomtyauwxhiv0c.png)
Now, let's interpret the result:
The solution
 indicates that any real number greater than
indicates that any real number greater than
 will satisfy the original inequality. To visualize this on a number line, we mark a circle at
will satisfy the original inequality. To visualize this on a number line, we mark a circle at
 and draw an arrow to the right, indicating all values greater than this point.
and draw an arrow to the right, indicating all values greater than this point.
In conclusion, the compound inequality
 represents a "greater than" relationship, and the solution set for
represents a "greater than" relationship, and the solution set for