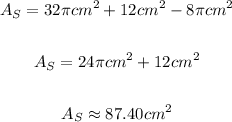Question

How do you find the area of the shaded region and using units

Answer 1

To find the area of the shaded region you divide the figure into:

2 semicircles and one triangle, as fllow:

First semicircle and triangle:

Second semicircle:

The area of the shaded area is the sum of Area 1 and 2 (semicircle and triangle) less the area of semicircle 3.

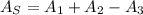
`A_S=A_1+A_2-A_3`Area 1:

The area of a semicircle is:

`A=(\pi\cdot r^2)/(2)`

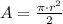
The semicirlce 1 has a diameter of (4cm+4cm+8cm=16cm) the radius is the half of the diameter (8cm):

Area 2:

The area of a triangle is:

The given triangle has height of 3cm and a base of 8cm:

Area 3:

The semicirlce has a diameter of 8cm, the radios os the hal od the diameter (4cm):

Then, the area of the shaded region is approximately: 87.40 squared centimeters
`\begin{gathered} A_S=32\pi cm^2+12cm^2-8\pi cm^2 \\ \\ A_S=24\pi cm^2+12cm^2 \\ \\ A_S\approx87.40cm^2 \end{gathered}`