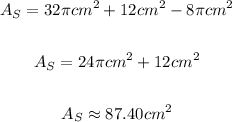To find the area of the shaded region you divide the figure into:
2 semicircles and one triangle, as fllow:
First semicircle and triangle:
Second semicircle:
The area of the shaded area is the sum of Area 1 and 2 (semicircle and triangle) less the area of semicircle 3.
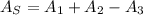
Area 1:
The area of a semicircle is:
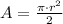
The semicirlce 1 has a diameter of (4cm+4cm+8cm=16cm) the radius is the half of the diameter (8cm):
![A_1=\frac{\pi\cdot(8\operatorname{cm})^2}{2}=(\pi64cm^2)/(2)=32\pi cm^2]()
Area 2:
The area of a triangle is:
![A=(1)/(2)b\cdot h]()
The given triangle has height of 3cm and a base of 8cm:
![A_2=(1)/(2)(8\operatorname{cm})(3\operatorname{cm})=(24cm^2)/(2)=12cm^2]()
Area 3:
The semicirlce has a diameter of 8cm, the radios os the hal od the diameter (4cm):
![A_3=\frac{\pi\cdot(4\operatorname{cm})^2}{2}=(\pi16cm^2)/(2)=8\pi cm^2]()
Then, the area of the shaded region is approximately: 87.40 squared centimeters