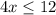the number
 is a solution to the following inequalities:
is a solution to the following inequalities:
-
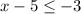
-
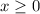
-
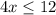
Therefore, option A,B and D are correct
Let's evaluate each inequality by substituting \( x = 0 \) to see if the inequality holds true.
1.
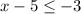
Substituting
 :
:
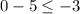
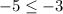
This inequality is true because
 is indeed less than or equal to
is indeed less than or equal to
 . Therefore,
. Therefore,
 is a solution to this inequality.
is a solution to this inequality.
2.
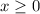
Substituting
 :
:
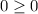
This inequality is also true because
 is equal to
is equal to
 . Therefore,
. Therefore,
 is a solution to this inequality.
is a solution to this inequality.
3.

Substituting
 :
:
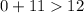
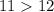
This inequality is false because \( 11 \) is not greater than \( 12 \). Therefore, \( x = 0 \) is not a solution to this inequality.
4.
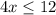
Substituting
 :
:
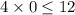

This inequality is true because
 is indeed less than or equal to
is indeed less than or equal to
 . Therefore,
. Therefore,
 is a solution to this inequality.
is a solution to this inequality.
5.
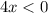
Substituting
 :
:
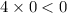

This inequality is false because
 is not less than
is not less than
 . Therefore,
. Therefore,
 is not a solution to this inequality.
is not a solution to this inequality.
In conclusion, the number
 is a solution to the following inequalities:
is a solution to the following inequalities:
-
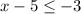
-
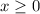
-