Mixed numbers
A mixed number is a way to write a fractional number that is greater than 1. Mixed numbers have two parts: an integer and a fraction smaller than 1. If the integer is a and the fraction is b/c then the mixed number can be written as a fraction following this procedure:
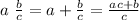
Simplifying
We must simplify this expression:

We can write both numbers as fractions using the formula above:
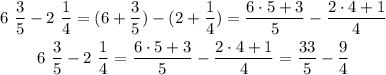
In order to perform the last substraction we can multiply and divide each fraction by the denominator of the other:
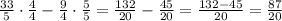
Now we have to write 87/20 as a mixed number. We can rewrite the numerator like this:
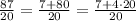
Then we distribute the division:
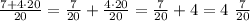
Then the answer is 4 7/20.