Question

2. Find the values of m and b so that the system has 2 solutions, no solutions, and one solution. y = x² y = mx + b

Answer 1

We have to find the values of m and b so that the system of equations have:

a) 2 solutions

b) no solution

c) one solution

We can start by writing the system of equations:

`\begin{gathered} y=x^2 \\ y=mx+b \end{gathered}`

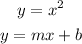
Then, we can write:

`\begin{gathered} x^2=mx+b \\ x^2-mx-b=0 \end{gathered}`

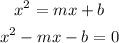
We have a quadratic equation, for which the solutions are the roots of the quadratic expression.

Then, we can write the roots as:

`\begin{gathered} x=\frac{-(-m)\pm\sqrt[]{(-m)^2-4\cdot1\cdot(-b)}}{2\cdot1} \\ x=\frac{m\pm\sqrt[]{m^2+4b}}{2} \end{gathered}`

We have the solutions for x in function of m and b.

The argument in the square root will give us the options that the question is asking:

a) We will have 2 solutions if the square root has an argument that is positive.

b) We will have no solution if the square root has an argument that is negative, becacuse there is no real solution for the square root of a negative number.

c) We will have one solution if the argument of the square root is 0.

Then, we start with one solution (point c):

`\begin{gathered} m^2+4b=0 \\ m^2=-4b \\ m=\sqrt[]{-4b} \end{gathered}`

If b=-1, then m is:

`m=\sqrt[]{-4(-1)}=\sqrt[]{4}=2`

Then, when m=2 and b=-1, we have one solution:

Now, we can find the range for which we won't have any solution.

As b is the y-intercept of the line, we can see from the graph that if keep m=2, we won't have any solution when b<-1.

We can check this from the statement that if the argument of the square root is less than 0, then we don't have any real solution:

`\begin{gathered} m^2+4b<0 \\ 2^2+4b<0 \\ 4+4b<0 \\ 4b<-4 \\ b<-1\longrightarrow\text{ no real solution} \end{gathered}`

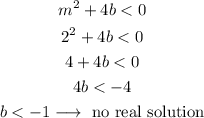
As we expected, when b<-1, we don't have any real solution.

For example, we can see it when b = -2:

The functions do not intersect. That indicates that the system does not have a solution.

In the same way, if m=2 and b>-1, we will have 2 solutions:

`\begin{gathered} m^2+4b>0 \\ 2^2+4b>0 \\ 4+4b>0 \\ 4b>-4 \\ b>-1\longrightarrow\text{two solutions} \end{gathered}`

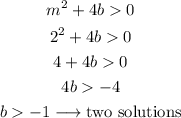
We can test this with m=2 and b=0:

Answer:

We have multiple solutions for m and b, but we will write a pair of values that satisfy the confitions for this system.

One solution: m=2, b=-1.

No solution: m=2, b=-2

Two solutions: m=2, b=0