Question

For the geometric sequence, find the sum of the specified number of terms.

The first 8 terms of 4, -12, 36, ...
S8=

Answer 1

Given:

The geometric sequence is

`4, -12, 36,...`

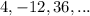
To find:

The sum of first 8 terms of the given geometric sequence.

Solution:

We have,

`4, -12, 36,...`

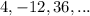
Here, the first term is 4 and the common ratio is

`r=(-12)/(4)`

`r=-3`

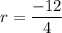
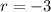
The sum of first n terms of a geometric sequence is

`S_n=(a(r^n-1))/(r-1)`

Where, a is the first term and r is the common ratio.

Putting n=8, a=4 and r=-3, we get

`S_8=(4((-3)^8-1))/(-3-1)`

`S_8=(4(6561-1))/(-4)`

`S_8=-6560`

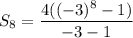
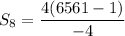
Therefore, the sum of first 8 terms is -6560.