Question

Write an equation of the line that passes through (-2, 4) that intersects the line 2 + 5 = 7 to form a right angle.

must show work

Answer 1

The equation of the line passing through (-2, 4) and forming a right angle with the line
`\(2x + 5y = 7\) is \(5x - 2y = 14\).`

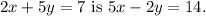
Step-by-step explanation:

To find the equation of the line passing through (-2, 4) and forming a right angle with
`\(2x + 5y = 7\),`we need to determine the slope of the given line.

The original line
`\(2x + 5y = 7\)` can be rewritten in slope-intercept form as
`\(y = -(2)/(5)x + (7)/(5)\).`

The negative reciprocal of this slope is
`\(m = (5)/(2)\),`which is the slope of the line perpendicular to the given line.

Next, use the point-slope form of a line
`\(y - y_1 = m(x - x_1)\), where \((x_1, y_1)\)` is the given point (-2, 4) and
`\(m\)`is the slope. Substitute the values to get
`\(y - 4 = (5)/(2)(x + 2)\)`.

Simplifying, we get
`\(5x - 2y = 14\),` which is the equation of the line passing through (-2, 4) and forming a right angle with
`\(2x + 5y = 7\).`

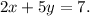
This is based on the property that the product of the slopes of two perpendicular lines is -1.

Therefore, knowing the slope of the given line allows us to find the slope of the perpendicular line that passes through a given point.

The final equation ensures that the two lines form a right angle at the point (-2, 4).