Question

Find the sum of the first 22 terms of the arithmetic sequence, the first term is - 2 and the common difference is -5.

Answer 1

The sum of the first 22 terms of the sequence is -1199.

Explanation:

Arithmetic sequence:

The general term of a arithmetic sequence is given by:

`A_n = a_1 + (n-1)r`

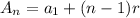
In which
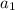`a_1` is the first term and r is the common difference.

The sum of the first n terms of a arithmetic sequence is given by:

`S_n = (n(a_1+a_n))/(2)`

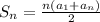
First term is - 2 and the common difference is -5.

This means that
`a_1 = -2, a_n = -5`

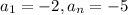
Sum of the first 22 terms

`S_(22) = (22(-2+a_(22)))/(2) = 11(-2+a_(22))`

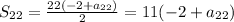
In which

`a_(22) = -2 + (22-1)(-5) = -107`

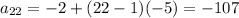
So

`S_(22) = 11(-2 - 107) = 11(-109) = -1199`

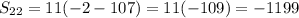
The sum of the first 22 terms of the sequence is -1199.