Final Answer:
To solve this problem, let's denote the side length of the metallic square frame as a. The area of the circle formed by bending the metallic square frame with 308 cm of perimeter is approximately 4687.38 cm².
Explanation:
To solve this problem, let's denote the side length of the metallic square frame as a. Since it's a square, all sides are equal. The perimeter (P) of the square is given by 4a, and in this case, it's equal to 308 cm:
4a = 308
To find a, we divide both sides by 4:
a =
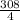
a = 77
Now that we know the side length (a = 77), we can find the radius (r) of the circle formed by using half of the diagonal of the square:
r =
 × a
× a
r =
 × 77
× 77
Now, the area (
 ) of a circle is given by
) of a circle is given by
 = πr²:
= πr²:
 = π
= π
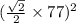
 = π ×
= π ×

 = π ×
= π ×
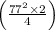
 =
=
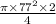
 =
=
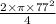
Now, calculating this gives:
 ≈ 4687.38 cm²
≈ 4687.38 cm²
Therefore, the area of the circle formed by bending the metallic square frame is approximately 4687.38 cm².