Question

What is the average rate of change of the function f(x)=−3x−19 over the interval [1, 3] ?

Enter your answer in the box.
average rate of change =

Answer 1

The average rate of change of the function (f(x) = -3x - 19) over the interval [1, 3] is -3.

Step-by-step explanation:

The average rate of change of a function over an interval [a, b] is given by the formula:
`\(\frac{{f(b) - f(a)}}{{b - a}}\)`. Applying this formula to the function (f(x) = -3x - 19) over the interval [1, 3], first, find the values of the function at x = 1 and x = 3.

(f(1) = -3(1) - 19 = -3 - 19 = -22) and (f(3) = -3(3) - 19 = -9 - 19 = -28).

Now, calculate the average rate of change using the formula:

`\(\frac{{f(3) - f(1)}}{{3 - 1}} = \frac{{-28 - (-22)}}{{3 - 1}} = \frac{{-28 + 22}}{2} = \frac{{-6}}{2} = -3\).`

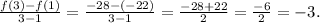
The average rate of change of -3 represents the constant rate at which the function \(f(x) = -3x - 19\) is changing over the interval [1, 3]. This means that on average, the function's output decreases by 3 units for every 1 unit increase in x within this interval. The negative sign indicates a decrease in the function's value as x increases, reflecting a downward trend in the function over the specified interval. This rate of change is consistent with the linear nature of the function, which has a constant slope of -3, indicating a steady decrease in value as x increases.