Answer:
The most correct option for the magnitude of the velocity of the ship relative to the port is;
33 km/h
Step-by-step explanation:
The given parameters of the cargo ship are;
The speed of the cargo ship = 25 km/h
The direction of the cargo ship, θ₁ = 20° North of East
The speed of the current = 10 km/h
The direction of the current, θ₂ = 15° North of East relative to the port
Therefore the direction of the ship relative to the port, 'θ', is given as the sum of θ₁ and θ₂ as follows;
θ = θ₁ + θ₂ = 20° + 15° = 35°
The component of the velocities relative to the port are given as follows;
The velocity of the ship, v₁ = 25·cos(35°)·i + 25·sin(35°)·j
The velocity of the current , v₂ = 10·cos(15°)·i + 10·sin(15°)·j
The velocity of the ship relative to the port, v = (25·cos(35°) + 10·cos(15°))·i + (25·sin(35°) + 10·sin(15°))·j
∴ v ≈ 30.14·i + 16.93·j
The magnitude of 'v' is
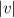 = √(30.14² + 16.93²) ≈ 34.6
= √(30.14² + 16.93²) ≈ 34.6
Therefore, the magnitude of the velocity of the ship relative to the port,
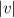 ≈ 34.6 km/h.
≈ 34.6 km/h.
Therefore, the closest correct option for the velocity of the ship relative to the port is 33 km/h