Question

HELP ASAP 40 POINTS

What is the equation for the nth term of the sequence
And what is the 52nd term of the sequence. -8,-12,-16

Answer 1

Given:

The sequence is -8, -12, -16.

To find:

The nth and 52th term of the given sequence.

Solution:

We have,

-8, -12, -16

It is an AP because the difference between consecutive terms are equal. Here, first term is -8 and the common difference is

`r=a_2-a_1`

`r=-12-(-8)`

`r=-12+8`

`r=-4`

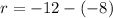
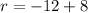
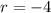
The nth term of an AP is

`a_n=a+(n-1)d`

Where, a is first term and d is common difference.

Putting a=-8 and d=-4, we get

`a_n=-8+(n-1)(-4)`

`a_n=-8-4n+4`

`a_n=-4-4n`

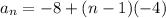
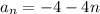
Putting n=52, we get

`a_(52)=-4-4(52)`

`a_(52)=-4-208`

`a_(52)=-212`

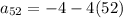
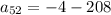
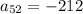
Therefore, the equation for the nth term of the given sequence is
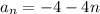`a_n=-4-4n` and the 52nd term of the sequence is -212.