Question

this is a 2 part questionCoffee To Go A person places a cup of coffee on the roof of his car while he dashes back into the house for a forgotten item. When he returns to the car, he hops in and takes off with the coffee cup still on the roof. (a) If the coefficient of static friction between the coffee cup and the roof of the car is 0.24, what is the maximum acceleration the car can have without causing the cup to slide? Ignore the effects of air resistance. (b) What is the smallest amount of time in which the person can accelerate the car from rest to15 m>s and still keep the coffee cup on the roof?

Answer 1

Given data

*The given coefficient of static friction between the coeffee cup and the roof of the car is

`\mu=0.24`

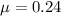
*The value of the acceleration due to gravity is g = 9.8 m/s^2

*The given initial speed of the car is u = 0 m/s

*The given final speed of the car is v = 15 m/s

(a)

The formula for the maximum acceleration of the car can have without causing the cup to slide is given as

`a=\mu g`

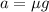
Substitute the known values in the above expression as

`\begin{gathered} a=(0.24)(9.8) \\ =2.35m/s^2 \end{gathered}`

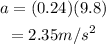
Hence, the maximum acceleration of the car can have without causing the cup to slide is a = 2.35 m/s^2

(b)

The formula for the smallest amount of time in which the person can accelerate the car from rest to 15 m/s is given by the equation of motion as

`\begin{gathered} v=u+at \\ t=(v-u)/(a) \end{gathered}`

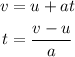
Substitute the known values in the above expression as

`\begin{gathered} t=(15-0)/(2.35) \\ =6.37\text{ s} \end{gathered}`

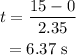
Hence, the smallest amount of time in which the person can accelerate the car from rest to 15 m/s is t = 6.37 s