Question

Two masses are connected by a string. One mass m₂ rests on a frictionless table, and the other mass m₁ is suspended from the edge of the table. The string passes over a frictionless pulley at the edge of the table

A. If m₁ = 50 g and m₂ = 100 g, what is the acceleration of the masses immediately after they are released from rest?
B. If 15 g is transferred from m₂ to m₁, such that m₁ = 65 g and m₂ = 85 g, what is the acceleration of the masses immediately after they are released from rest?

Answer 1

A. The acceleration of the masses, immediately after they are released from rest, is approximately
`\(1.96 \, \text{m/s}^2\) when \(m_1 = 50 \, \text{g}\) and \(m_2 = 100 \, \text{g}\).`

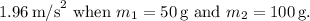
B. After transferring 15 g from
`\(m_2\) to \(m_1\) such that \(m_1 = 65 \, \text{g}\) and \(m_2 = 85 \, \text{g}\),` the acceleration of the masses, immediately after release, becomes approximately
`\(2.72 \, \text{m/s}^2\).`

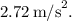
Step-by-step explanation:

A. The acceleration of the masses in a system with a mass hanging off a table and connected by a string passing over a pulley is determined by the difference in the masses. The formula for acceleration
`(\(a\))` is given by
`\(a = (m_2 - m_1)/(m_1 + m_2) * g\),` where
`\(g\)` is the acceleration due to gravity
`(\(9.8 \, \text{m/s}^2\)).` Substituting the given values, we get
`\(a = (100 - 50)/(100 + 50) * 9.8 \approx 1.96 \, \text{m/s}^2\).`

B. After transferring 15 g from
`\(m_2\) to \(m_1\)`, the masses become
`\(m_1 = 65 \, \text{g}\)` and
`\(m_2 = 85 \, \text{g}\).` Using the same formula for acceleration, we find
`\(a = (85 - 65)/(85 + 65) * 9.8 \approx 2.72 \, \text{m/s}^2\).`

Understanding the dynamics of connected masses, particularly in scenarios involving pulleys and inclined planes, is essential in physics. The acceleration formula provides insights into how the masses interact and move in response to gravitational forces. The transfer of mass between
`\(m_1\) and \(m_2\)` alters the system's acceleration, showcasing the principles of Newtonian mechanics.