Question

Tomas works for a cellphone company. he has a base salary of $350 each month and earns an additional $40 for each cellphone he sells. write a function (linear equation) in slope-intercept form (y = mx + b) that represents tomas' total earnings (y) for one month for selling (x) number of cellphones.

Use the linear equation from question 1 to determine Tomas' earnings for a month where he sold 30 cellphones. *

Answer 1

The function is
`y = 40x + 350`

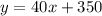
When he sold 30 cellphones, he earned $1550.

Explanation:

Equation of a line:

The equation of a line has the following format:

`y = mx + b`

In which m is the slope(how much y changes when x changes by 1), and b is the y-intercept, that is, the value of w when x = 0.

Base salary of $350 each month and earns an additional $40 for each cellphone he sells.

If he sells 0 cellphones, he earns $350, so
`b = 350`.

For each cellphone he sells, he earns $40, so
`m = 40`

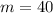
The function is:

`y = mx + b = 40x + 350`

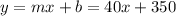
Tomas' earnings for a month where he sold 30 cellphones.

This is y when
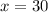`x = 30`. So

`y = 40*30 + 350 = 1550`

When he sold 30 cellphones, he earned $1550.