Answer:
h = 18.88 inches
Explanation:
Given that,
The circumference of a cylinder is 20 inches
The volume of the cylinder, V = 600 cubic inches
We need to find the height of the cylinder. We know that the volume of a cylinder is given by :
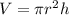
r is radius
We know that,
circumference = 2πr
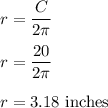
So,
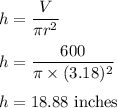
So, the height of the cylinder is 18.88 inches.