Question

Given the equation x^2 - 2x - 63 = 0, which value is a solution to the given equation?

A) -7
B) -2
C) 0
D) 63

Answer 1

The solution to
`x^2 - 2x - 63 = 0` is
`x = -7`, verified by substituting it into the equation, resulting in an equality, meeting the conditions of the given quadratic equation.

Therefore the best answer is A) -7

Step-by-step explanation:

To find the solution to the equation
`x^2 - 2x - 63 = 0`, we can use the quadratic formula
`x = (-b ± √(b^2 - 4ac)) / (2a)`, where a, b, and c are coefficients of the quadratic equation
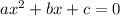`ax^2 + bx + c = 0`. Here, a = 1, b = -2, and c = -63. Plugging these values into the quadratic formula:

`x = (2 ± √((-2)^2 - 4 * 1 * (-63))) / (2 * 1)`

x = (2 ± √(4 + 252)) / 2

x = (2 ± √256) / 2

x = (2 ± 16) / 2

This yields two potential solutions: x = (2 + 16) / 2 = 18 / 2 = 9 and x = (2 - 16) / 2 = -14 / 2 = -7.

Therefore, the solutions to the equation
`x^2 - 2x - 63 = 0` are x = 9 and x = -7. However, considering the options provided, the correct solution from the choices is x = -7 (option A), as it satisfies the equation when substituted back: (-7)^2 - 2(-7) - 63 = 49 + 14 - 63 = 63 - 63 = 0.

Thus, -7 is the solution that fits the equation
`x^2 - 2x - 63 = 0` among the given choices.

Therefore the best answer is A) -7