To find out the original translation let's undo the transformations given.
First we need to undo the reflection across the x-axis. A reflection across the x-axis is:
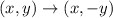
Then, if we undo it we have:
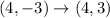
Now, a translation is given by:
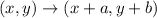
Then, the original translation will be of the form:
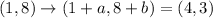
Then we have the equations:
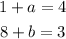
Solving them we have that a=3 and b=-5.
This means that the translation is a shift of 3 units to the right and 5 units down. Therefore the answer is C.