Question

11)The Point (1, 8) was translated in the coordinate plane and then reflected across the x-axis. It's final image was had the coordinates (4, -3) Which of the following best describes the translation that occurred? A)a shift of 3 units to the right and 11 units down B)a shift of 8 units left and 2 units down C)a shift of three units to the right and 5 units down D) a shifted 2 units left and 4 units up

Answer 1

To find out the original translation let's undo the transformations given.

First we need to undo the reflection across the x-axis. A reflection across the x-axis is:

`(x,y)\rightarrow(x,-y)`

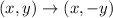
Then, if we undo it we have:

`(4,-3)\rightarrow(4,3)`

Now, a translation is given by:

`(x,y)\rightarrow(x+a,y+b)`

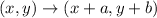
Then, the original translation will be of the form:

`(1,8)\rightarrow(1+a,8+b)=(4,3)`

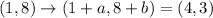
Then we have the equations:

`\begin{gathered} 1+a=4 \\ 8+b=3 \end{gathered}`

Solving them we have that a=3 and b=-5.

This means that the translation is a shift of 3 units to the right and 5 units down. Therefore the answer is C.