Question

An insulating sphere of radiusstudent submitted image, transcription available below,centered at the origin, has a uniform volume charge densitystudent submitted image, transcription available below.

A spherical cavity is excised from the inside of the sphere.The cavity has radiusstudent submitted image, transcription available belowand is centered at positionstudent submitted image, transcription available below, wherestudent submitted image, transcription available below, so that the entire cavity is contained within thelarger sphere. Find the electric field inside the cavity.
Express your answer as a vector interms of any or all ofstudent submitted image, transcription available below,student submitted image, transcription available below,student submitted image, transcription available below, andstudent submitted image, transcription available below.

Answer 1

The electric field (E) inside the cavity is given by the formula: E = (k * Q * r) / R³, where k is the Coulomb constant, Q is the total charge of the insulating sphere, r is the position vector pointing from the center of the sphere to the point within the cavity, and R is the radius of the insulating sphere.

Step-by-step explanation:

The electric field inside a spherical cavity within a uniformly charged sphere is influenced by the charge distribution. In this scenario, we can use Gauss's Law to determine the electric field. The formula for the electric field (E) inside the cavity is expressed as: E = (k * Q * r) / R³, where k is the Coulomb constant (8.99 ×
`10^9`
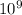
`N m^2/C^2`), Q is the total charge of the insulating sphere, r is the position vector pointing from the center of the sphere to the point within the cavity, and R is the radius of the insulating sphere.

The key factor in this expression is the position vector (r), which describes the location within the cavity. The electric field is directed along this vector. As r changes, the magnitude and direction of the electric field at different points within the cavity will vary.

In summary, the electric field within the spherical cavity is determined by the given formula, which accounts for the charge distribution of the insulating sphere and the position within the cavity. The vector nature of r ensures the correct direction of the electric field at any point within the cavity.