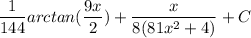Question

How do I evaluate this using trigonometric substitution?

∫dx/(81x^2+4)^2

Answer 1

`\displaystyle (1)/(144)arctan((9x)/(2)) + (x)/(8(81x^2 + 4)) + C`

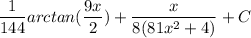
General Formulas and Concepts:

Alg I

• Terms/Coefficients
• Factor
• Exponential Rule [Dividing]:
  `\displaystyle (b^m)/(b^n) = b^(m - n)`

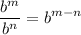
Pre-Calc

[Right Triangle Only] Pythagorean Theorem: a² + b² = c²

• a is a leg
• b is a leg
• c is hypotenuse

Trigonometric Ratio:
`\displaystyle sec(\theta) = (1)/(cos(\theta))`

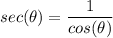
Trigonometric Identity:
`\displaystyle tan^2\theta + 1 = sec^2\theta`

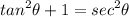
TI:
`\displaystyle sin(2x) = 2sin(x)cos(x)`

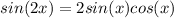
TI:
`\displaystyle cos^2(\theta) = (cos(2x) + 1)/(2)`

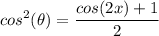
Calc

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

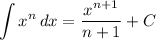
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

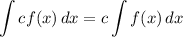
IP [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

U-Substitution

U-Trig Substitution: x² + a² → x = atanθ

Explanation:

Step 1: Define

`\displaystyle \int {(dx)/((81x^2 + 4)^2)}`

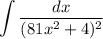
Step 2: Identify Sub Variables Pt.1

Rewrite integral [factor expression]:

`\displaystyle \int {(dx)/([(9x)^2 + 4]^2)}`

Identify u-trig sub:

`\displaystyle x = atan\theta\\9x = 2tan\theta \rightarrow x = (2)/(9)tan\theta\\dx = (2)/(9)sec^2\theta d\theta`

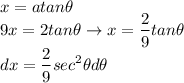
Later, back-sub θ (integrate w/ respect to x):

`\displaystyle tan\theta = (9x)/(2) \rightarrow \theta = arctan((9x)/(2))`

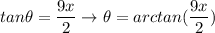
Step 3: Integrate Pt.1

1. [Int] Sub u-trig variables:
   `\displaystyle \int {((2)/(9)sec^2\theta)/([(2tan\theta)^2 + 4]^2)} \ d\theta`
2. [Int] Rewrite [Int Prop - MC]:
   `\displaystyle (2)/(9) \int {(sec^2\theta)/([(2tan\theta)^2 + 4]^2)} \ d\theta`
3. [Int] Evaluate exponents:
   `\displaystyle (2)/(9) \int {(sec^2\theta)/([4tan^2\theta + 4]^2)} \ d\theta`
4. [Int] Factor:
   `\displaystyle (2)/(9) \int {(sec^2\theta)/([4(tan^2\theta + 1)]^2)} \ d\theta`
5. [Int] Rewrite [TI]:
   `\displaystyle (2)/(9) \int {(sec^2\theta)/([4sec^2\theta]^2)} \ d\theta`
6. [Int] Evaluate exponents:
   `\displaystyle (2)/(9) \int {(sec^2\theta)/(16sec^4\theta) \ d\theta`
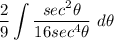
7. [Int] Rewrite [Int Prop - MC]:
   `\displaystyle (1)/(72) \int {(sec^2\theta)/(sec^4\theta) \ d\theta`
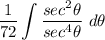
8. [Int] Divide [ER - D]:
   `\displaystyle (1)/(72) \int {(1)/(sec^2\theta) \ d\theta`
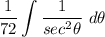
9. [Int] Rewrite [TR]:
   `\displaystyle (1)/(72) \int {cos^2\theta} \ d\theta`
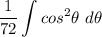
10. [Int] Rewrite [TI]:
    `\displaystyle (1)/(72) \int {(cos(2\theta) + 1)/(2)} \ d\theta`
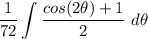
11. [Int] Rewrite [Int Prop - MC]:
    `\displaystyle (1)/(144) \int {cos(2\theta) + 1} \ d\theta`
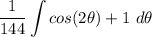
12. [Int] Rewrite [Int Prop - A/S]:
    `\displaystyle (1)/(144) [\int {cos(2\theta) \ d\theta + \int {1} \ d\theta]`

Step 4: Identify Sub Variables Pt.2

Determine u-sub for trig int:

u = 2θ

du = 2dθ

Step 5: Integrate Pt.2

1. [Ints] Rewrite [Int Prop - MC]:
   `\displaystyle (1)/(144) [(1)/(2) \int {2cos(2\theta) \ d\theta + \int {1 \theta ^0} \ d\theta]`
2. [Int] U-Sub:
   `\displaystyle (1)/(144) [(1)/(2) \int {cos(u) \ du + \int {1 \theta ^0} \ d\theta]`
3. [Ints] Integrate [Trig/Int Rule - RPR]:
   `\displaystyle (1)/(144) [(1)/(2) sin(u) + \theta + C]`
4. [Expression] Back Sub:
   `\displaystyle (1)/(144) [(1)/(2) sin(2 \theta) + arctan((9x)/(2)) + C]`
5. [Exp] Rewrite [TI]:
   `\displaystyle (1)/(144) [(1)/(2)(2sin(\theta)cos(\theta)) + arctan((9x)/(2)) + C]`
6. [Exp] Multiply:
   `\displaystyle (1)/(144) [sin(\theta)cos(\theta) + arctan((9x)/(2)) + C]`
7. [Exp] Back Sub:
   `\displaystyle (1)/(144) [sin(arctan((9x)/(2)))cos(arctan((9x)/(2))) + arctan((9x)/(2)) + C]`

Step 6: Triangle

Find trig values:

`\displaystyle tan\theta = (9x)/(2)`

`\displaystyle \theta = arctan((9x)/(2))`

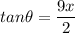
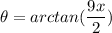
tanθ = opposite / adjacent; solve hypotenuse of right triangle, determine trig ratios:

sinθ = opposite / hypotenuse

cosθ = adjacent / hypotenuse

Leg a = 2

Leg b = 9x

Leg c = ?

1. Sub variables [PT]:
   `\displaystyle 2^2 + (9x)^2 = c^2`
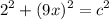
2. Evaluate exponents:
   `\displaystyle 4 + 81x^2 = c^2`
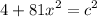
3. [Equality Property] Square root both sides:
   `\displaystyle √(4 + 81x^2) = c`
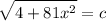
4. Rewrite:
   `c = √(81x^2 + 4)`

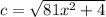
Substitute into trig ratios:

`\displaystyle sin\theta = (9x)/(√(81x^2 + 4))`

`\displaystyle cos\theta = (2)/(√(81x^2 + 4))`

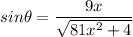
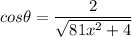
Step 7: Integrate Pt.3

1. [Exp] Sub variables [TR]:
   `\displaystyle (1)/(144) [(9x)/(√(81x^2 + 4)) \cdot (2)/(√(81x^2 + 4)) + arctan((9x)/(2)) + C]`
2. [Exp] Multiply:
   `\displaystyle (1)/(144) [(18x)/(81x^2 + 4) + arctan((9x)/(2)) + C]`
3. [Exp] Distribute:
   `\displaystyle (1)/(144)arctan((9x)/(2)) + (x)/(8(81x^2 + 4)) + C`